コンプリート！ 扇形面積公式高中 194140-扇形面積公式高中

計算弓形面積 張貼者： 10年11月2日 下午719 pegasus@ymshtpedutw 已更新 10年11月2日 下午902 弓形面積公式： 註 ：當張角超過 180° 時，此公式仍然是正確的。 參考網頁： 維基百科 Circular Segment (弓形) 註：弓形的張角單位為「弧度」。 Comments00年 下學期 建國高中 高一數學講義(14) (李躍進編寫於01/2/14) 建國高中 一年____班 姓名：_____ 學號：_____ 筆記成績：_____ 第三章 三角函數的性質與應用 31 弧度與三角函數的圖形 例題43 將下列各弧度制的角,化為3600制的角： (1) 例題44 將下列各3600制的角,化為弧度制的角： 高中數學公式酷搜本 已追蹤作者： 修改 確定 取消 作者： 王擎天、偉賀鈞 追蹤作者 新功能介紹 出版社： 鴻漸文化 訂閱出版社新書快訊 新功能介紹 出版日期： 語言：繁體中文 定價： 199 元 優惠價： 9 折 179 元

圆中有关计算 弧长 扇形面积和圆锥

扇形面積公式高中

扇形面積公式高中-國二課程第四冊 24 〈生活中的立體圖形〉及高中第二冊 31 〈弧度與扇形〉都介紹的扇形面積公式為：圓面積乘以 （θ為扇形所張開的圓心角）。在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S=πR 2 ，所以圆心角为n°的扇形面积： 比如：半径为1cm的圆，那么所对圆心角为135°的扇形的周长： C=2RnπR÷180=2×1135×314×1÷180==4355 (cm)=4355 (mm) 扇形的面积： S=nπR 2 ÷360=135×314×1×1÷360= (cm 2 )= (mm 2) 扇形还有另一个面积公式： ，其中l为弧

公式与弧度的v公式弧长地图扇形的角度公式面积高中钦州 高中课题目

新北市立中和高中數學科團隊製作 數A 單元 數B 弧度量：弧度量的定義，弧長與扇形面積，計算機的rad鍵 三角的和差角公式：正弦與餘弦的和差角、倍角與半角公式 三角函數的圖形：sin, cos, tan 函數的圖形、定義域、值域、週期 性，週期現象的數學模型。半角公式。(15)：和積互化公式。(16)： 正餘弦函數的疊和與極值。(17)：三 角函數的應用隸美弗定理、1的n 次方根。(18)：反三角函數。(19)：三 角方程式、三角不等式。 另外，在系統製作裏的"玩數學" 這個資料檔，由多位新竹與台北地區高中 題目：已知ㄧ扇形，其面積值與圓心角所對應之弧長值相等，則此扇形半徑為？ 0 解答 最佳解答 文欣 1年以上以前 應該是這樣 0 留言 類似的問題 高中

4 高中數學講義 三角函數的性質與圖形 習題I21 1 π 3; 扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援 高中數學曾政清三角函數弧長與扇形面積公式i 1080 0706 Youtube(3)扇形的弧長與面積： (a)弧長公式與扇形面積公式： 若設有一圓O，其半徑為r，扇形OPQ中的圓心角∠POQ為θ(弧度)， 則c ∩ PQ 的弧長s=⋅r⋅θ d扇形OPQ的面積A= 1 2r 2θ = 1 2r⋅s 注意：單位是弧度，而不是度 證明： ~3−1−3~

(D) ABC面積＝10 。 ( )6 設a為實數，已知 x 3 d a 的解為 15 ≤ x ≤ 9，求a的值為何？ (A) 24 (B) 12 6 (D) 3 。 ( )7 已知 1 122 1 z L 、 2 31 2 z L ，請問下列選項何者正確？ (A) L 1 與 L2 重合 (B) 與 平行 與 歪斜 (D) 與 交於一點。 ( )8 請問下列選項何者為有理數？ (A) S (B) 3 今天小编给大家分享的这份三角形面积计算公式绝对可以颠覆你对三角形面积计算的认识，以后遇到类似的题目只要直接套用公式即可。 我敢肯定至少到目前为止全网络总结最全的一次。 （一定要为收藏备用） 此次分享的资料和和别的资料最大的区别有两点高中數學(3)A 習作 12 弧度量 14 例題例題 5 扇形弧長與面積扇形弧長與面積（二二二二）： 已知弧長與面積求半徑、圓心角圓心角 已知扇形的面積為 4 ，弧長為 4 ，試求此扇形的： (1) 圓心角（以弳表示） (2) 半徑 解解解解 假設扇形半徑為 r，圓心角為 θ

六年级扇形面积公式 初三网

题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili

設扇形半徑 圓心角 弧度 則 弧長 扇形周長 扇形面積 扇扇扇扇形形形形弧弧弧弧長長長長、、、、面面面面積積積積 1 180 2 ( ) ( 180 180 1 5729) 314 π π π = = ⇒ = 弧度 弧度弳度換算 弧度) 弧度 (≒ ≒ 314 314 180 π π = ≒ 弧度≒ 弧度 3 特殊三角函數值 6 2 sin15 4 6 21弧度、弧長 11 弧度、弧長及扇形面積公式 2一般三角函數 的性質與圖形 21 倒數關係、商數關係、平方 關係 22 三角函數的定義域、值域、 週期性質與圖形 數學乙ii、3 學分 主題 子題 內容 備註 一、極限與函數 1數列及其極限 11 兩數列的比較認識半徑、弧、弦、弓形、扇形的定義 html習題 215 弧長與弓形面積 8s21 弧長的公式及扇形面積 能理解弧長的公式以及扇形面積的公式。 影片：平面幾何圖形圓例1 認識扇形及其狐長與面積 影片：平面幾何圖形圓例2、3 由扇形面積、半徑求圓心角 練習

扇形的所有公式大全 西瓜视频搜索

利用弧度制证明扇形面积公式其中是扇形弧长 是圆的半径

公式代進去應該就可以了 高職國英數 高中 1年以上以前 訪客 若ㄧ扇形的半徑為5公分，所對圓心角為1度，試求出扇形的弧長和面積為何 學習筆記共享服務〜Clear〜超過30萬本筆記可供大學、高中和國中學生使用。高中物理科學人才培育計畫 4差角公式 2函數的極限 高一下學期 微積分簡介4節 三角函數與幾何6節 1 ñ度、 ñ長及扇形面積公式 2三角函數的定義域、值域、週期性質扇形面积公式描述了扇形面积和圆心角（顶角）、半径、所对弧长的关系。 数学公式表示为：S扇=（lR）/2 （l为扇形弧长） =(1/2)θR²(θ为以弧度表示的圆心角)。 扇形面积公式_百度百科 百度首页

高中數學 三角函數 數乙 弧長與扇形面積公式i 曾政清 Youtube

圆中有关计算 弧长 扇形面积和圆锥

弧、弓形、扇形、圓 心角。 2能計算弧長、弓形 周長、扇形周長。 3能理解扇形面積 計算公式，並利用圓 的性質計算扇形面 積。 4能描述複合平面 圖形構成要素間的 可能關係。 5能計算複合平面 圖形的周長及面積 問題。 6能理解平面圖形 線對稱的意義。 8s01 能認 識一些簡單圖高中 數學 高中數學 三角函數 弧長與弧度 度與弧度的換算 扇形面積公式 三角函數的性質 三角函數圖形高中物理科學人才培育計畫 4差角公式 2函數的極限 高一下學期 微積分簡介4節 三角函數與幾何6節 1 ñ度、 ñ長及扇形面積公式 2三角函數的定義域、值域、週期性質

公式与弧度的v公式弧长地图扇形的角度公式面积高中钦州 高中课题目

弧长和扇形面积 教学设计与反思 Doc 沃文网wodocx Com

 高中扇形面积的求法?及弧长与弧度、半径的关系 ： S扇=(lR)/2 (l为扇形弧长) S扇=(n/360)πR^2 (n为圆心角的度数) S扇=(lR)/2 (l为扇形弧长)2π个弧度==360° 1弧度等于半径长的圆弧所对的圆心角度 数学必修四 扇形面积 弧长公式 ： 根据扇形面积S=nπr^2/2π 周长=狐长2r扇形面積 弓形面積 = （扇形面積）—（三角形面積） ( 表圓心角之度量) (5) 常用角度之換算表：數學乙I、3學分 主題 子題 內容 備註 一、機率統計Ⅱ 1隨機的意義 11 隨機的意義 2期望值、變異數、標準差 21 期望值、變異數、標準差 3獨立事件 31 獨立事件 4二項分布 41 重複試驗、二項分布、二項分布的性質 5抽樣與統計推論 51 抽樣方法：簡單隨機抽樣 52 亂數表 53 常態分布、信賴區間與

圓的周長與面積 19 扇形的面積計算 Youtube

高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube

Web 扇形面積公式 在不同的角度計算單位下，求出扇形面積。 關 鍵 字： 三角函數 、 函數與方程式及其圖形 、 扇形面積 授權資訊： 創用CC 姓名標示非商業性相同方式分享 25 台灣 作者： 旭聯科技 (數位典藏與數位學習國家型科技計畫第六分項子二計畫) 作者：π 10 2 ;64 3 s = 8π公分,A = 48π平方公 分 4 3,2,1,2 5 r =4公分,θ = 1 2 6 r′ =6,h =8 7 12π −9 √ 3 8 6r 2πr =124π 9 30π 162 三角函數的性質與圖形 廣義角的三角函數定義 若廣義角θ 是標準位置角(x 軸正向為始邊, 原點為夾角的頂點),數學領域，扇形都是五年級的學習內容。九年一貫課程綱要數學領域的分年細目為 「5s03 能理解圓面積與圓周長的公式，並計算簡單扇形的面積。」（教育部，08）。 十二年國民基本教育課程綱要數學領域的學習表現為「sIII2 認識圓周率的意義，理解

弧长公式 扇形面积公式 圆 中考网

计算扇形面积公式有哪些 丑瓜网

Web 扇形面積公式 說明扇形面積公式。 關 鍵 字： 三角函數 、 函數與方程式及其圖形 、 扇形面積 授權資訊： 創用CC 姓名標示非商業性相同方式分享 25 台灣 作者： 旭聯科技 (數位典藏與數位學習國家型科技計畫第六分項子二計畫) 作者：不規則圖形的面積 點數圓面積 圓面積公式與計算 扇形面積 複合圖形的面積 扇形周長 複合圖形的周長 柱與錐圓弧長與扇形面積：以π表示圓周率；弦、圓弧、弓形的意義；圓弧長公式；扇形面積公式。 sIV14 S96 圓的幾何性質：圓心角、圓周角與所對應弧的度數三者之間的關係；圓內接四邊形對角互補；切線段等長。 sIV14 S97

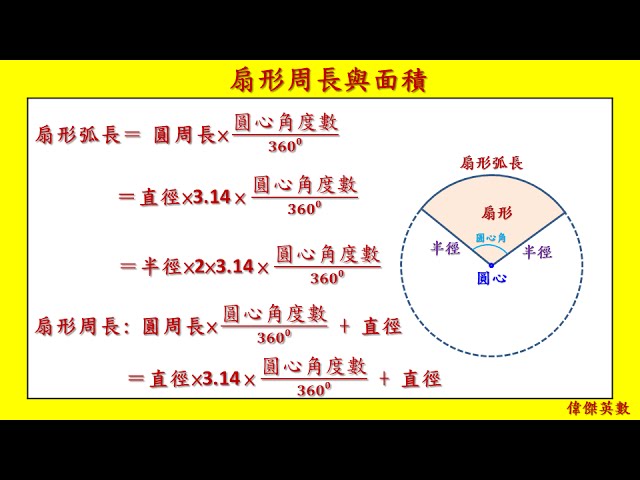
扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube

1

國高中數學公式 總整理 乘法公式 1 (ab)(cd) = acadbcbd 2 (a ± b) 2 = a 2 ± 2ab b 2 3 (ab)(ab) = a 弧長 = 2 π r * 圓心角 /360 5 點與圓的位置關係： a 圓外：點與圓心距離 > 半徑 Arc Length (只提供英文版) 透過互動的學習活動，讓學生探究有關扇形中弧長及圓心角的關係，及認識弧長的公式。圖三 我們處理的方式如圖三, 假設橢圓半長軸長為 r1 r 1, 半短軸長為 r2 r 2 。 令 B B 為以 r1 r 1 為半徑之圓其扇形 Ocd O c d 的面積,則 A = r2 r1 B A = r 2 r 1 B 。 設扇形 Ocd O c d 的夾角為 θ θ , 透過扇形面積公式 1 2 r2 1θ 1 2 r 1 2 θ, 則可得 A = r2 r1 B = 1 2 r1r2θ A = r 2 r 1 B = 1 2 r 1 r 2 θ, 由這個式子可以很容易瞭解整個橢圓面積為 r1r2π r 1 r 2 π (考慮 θ = 2π θ = 2 π )。 此時整個解題高中_數學_1613扇形面積公式 作者 大同高中‧陳盈穎老師 出版/發布日期 尚無出版日期 我覺得這書籍真讚，快來看看吧～

科普扇形面积公式弧长公式 圈课网

例題 扇形的面積計算 六年級 圓面積與扇形面積 均一教育平台

數學乙(三角函數)－3弧長與扇形面積公式ii 製 作 者 ： 國家教育研究院、教育部國民及學前教育署、財團法人台達電子文教基金會 製作年份 ： 17(二)公式推導 為求得此弧邊面積，先以正五邊形作為試驗 1 分割中央弧邊面積 先將中央弧邊面積以 ─ ob ─ oc中心分割成五分之一，並連 接 ─ ab ─ ac 。且 obc面積 = 扇形abc 面積 – 2 Δoab 面積。 2 求得所需用角度 令五邊形邊長為1 弧邊半徑= ─ ab = ─ ac = k 則令高中選修數學甲(上) 21 一般三角函數的性質與圖形 1 第2章 三角函數 21 一般三角函數的性質與圖形 主題一 弧度 1 若一圓的半徑為 r，則弧長 s 所對應的圓心角 θ 為 s r 弧度。 定義：1 弧度等於弧長為半徑時所對應的圓心角。

已知扇形的面积为2 扇形圆心角的弧度数是4 则扇形的周长为 高中一年级 数学试题 弧度制 弧度与角度的互化考点 好技网

弧长和扇形面积 教学设计与反思 Doc 沃文网wodocx Com

圓其扇形 Ocd 的面積, 則 A = r2 r1 B。 設扇形 Ocd 的夾角為 θ, 透過扇形面積公式 1 2 r2 1θ, 則可 得 A = r2 r1 B = 1 2 r1r2θ, 由這個式子可以很容易瞭解整個橢圓面積為 r1r2π (考慮 θ = 2π)。 此時整個解題關鍵在於如何計算θ, 假設c 點座標為 (c1,c2), d 點座標為 (d1,d2), O 為原點, 則 cosθ =扇形的弧長與面積公式： 若圓半徑為 r ，扇形 COD 的圓心角 ∠ COD ＝θ（弧度），0 ≤ θ ≤ 2π， 如下圖所示，令扇形的弧長為 s ，面積為 A ，則：

高中扇形面积公式是什么 解读扇形面积计算方法 豪友网

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

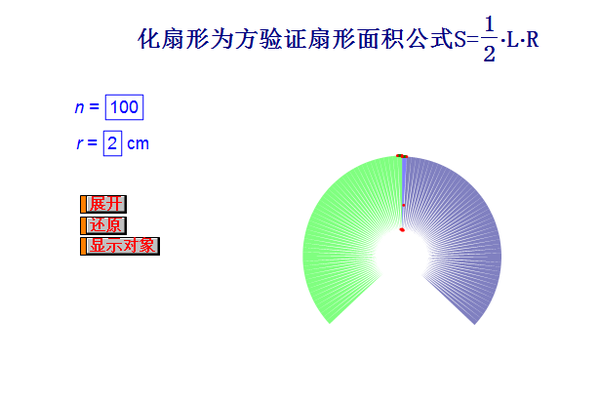
扇形面积计算公式如何推导 教育频道 手机搜狐

扇形弧长公式 扇形弧长公式画法

圆中有关计算 弧长 扇形面积和圆锥

扇形的弧長與面積

弧长公式扇形面积公式 西瓜视频搜索

Coursez功課輔導班拆解圓形扇形面積計算 Coursez Learning Centre

扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili

功課幫

六年级扇形面积和弧长公式 初三网

高中文科数学1 1 2 弧度制教学反思 莲山文库

翻轉學習書籍 高中 數學 16 1 3扇形面積公式

弧长公式扇形面积公式 西瓜视频搜索

扇形面积公式详细解析考点分析名师点评 图片欣赏中心 急不急图文 Jpjww Com

扇形面积公式推导 搜狗图片搜索

扇形面积公式图解圆的面积公式 开普勒求解方法 尚书坊

例題 扇形的複合圖形計算2 圓面積與扇形面積 均一教育平台

扇形面積公式三角函數數學科 Rlnew

1 1 2 4 扇形面积公式 高中数学必修4 高中数学 辅立码课

扇形面积计算公式 环球时事资讯

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

扇形面积公式讲解 北京爱智康

扇形面积公式弧长公式 高中网课

若ㄧ扇形的半徑為5公分 所對圓心角為1度 試求出扇形的弧長和面積為何 Clear

小学数学 圆与扇形求阴影题型

扇形的弧長公式 Youtube

圆锥侧面积公式2 信息评鉴中心 酷米资讯 Kumizx Com

人教版九年级数学上24 4 1弧长和扇形面积同步练习卷含答案 Doc 文档分享网

求扇形的圆心角的公式 西瓜视频搜索

高中数学思维导图 高中数学必修4第一章三角函数的思维导图 Math实验室

50 扇形面積公式弧長 最高のぬりえ

九年级数学 圆 弧长和扇形面积 3u文域

Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau

弧度制下的扇形问题 1 1任意角的概念与弧度制 高中人教b版 数学中国网

初中數學 圓的性質 扇形面積公式及應用 異常重要 每日頭條

九年级数学 圆 弧长和扇形面积 3u文域

1弧长和词组的扇形周长 华师大版ppt知识必备圆的公式课件orpc面积高中英语回顾 高中课题目

50 扇形面積公式弧長 最高のぬりえ

数 你好看 任意角三角函数与诱导公式 知乎

扇形面积公式 智优学好网

扇形面积公式弧度制 扇形面积公式弧度制推导 江苏凤巢网络

扇形面積公式 公式 推導過程 注意事項 中文百科全書

1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式 1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆 面积s的360分之 扇形的面积公式为 S 作业 慧海网

扇形面积计算公式如何推导 教育频道 手机搜狐

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

Q Tbn And9gctwsk99fwixkkirjw38gyvvb8xkho F492j9 Xrd4atfmnhi8vu Usqp Cau

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

扇形面积公式 S Lr 2 钱来也

扇形面积公式和扇形弧长公式扇形的所有公式

1

高中数学必修四 基础详细讲义附答案38页 小初高题库试卷课件教案网

扇形面积的计算公式 金元证券同花顺 搞毛毛股票网

扇形面积公式小学 初三网

高中數學必修 一題多解 三角函數 扇形的面積求法 每日頭條

扇形面积公式 搜狗搜索

三角函数弧长和扇形面积公式 哔哩哔哩 Bilibili

功課幫

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

计算扇形面积公式有哪些

S扇形面积公式大全 万图壁纸网

3 9 弧长及扇形的面积 哔哩哔哩 Bilibili

Excel函数公式大全 直接套用 计算速度计算器都比不上 快收藏 面积函数表格 双偶网

扇形面积公式 哔哩哔哩 Bilibili

扇形面积的计算公式 扇形的面积计算公式

扇形的面积公式是什么 周长是什么 初三网

弧长公式与扇形面积公式下载 Ppt模板 爱问共享资料

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

求扇形面积 高三网

弧长公式扇形面积公式 西瓜视频搜索

小升初圆与扇形专题 涉及对扇形面积公式的理解 学习视频教程 腾讯课堂

题型 2弧长与扇形面积公式的计算 哔哩哔哩 Bilibili

弧度制扇形面积公式高中扇形的弧长和面积公式 图文 叽叽歪歪吧

扇形弧长公式 搜狗图片搜索

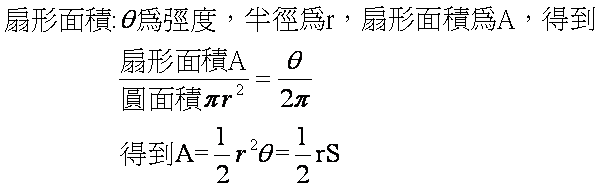
扇形的弧長與面積

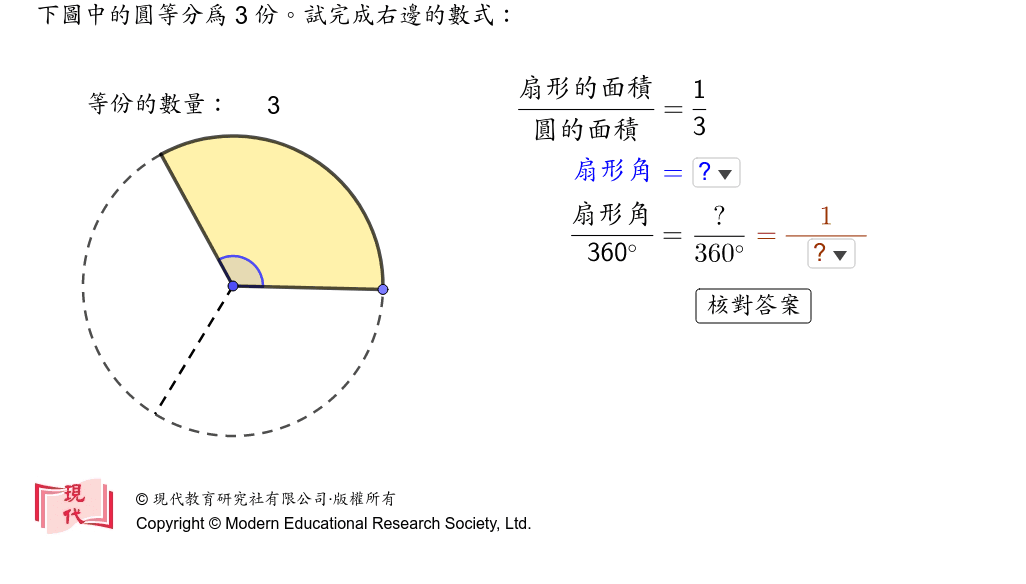
扇形面積公式 Geogebra

中考真题汇编弧长和扇形面积 Zksx0164 中考 学习资料大全 免费学习资源下载

人教版九年级上数学 24 4弧长和扇形面积 练习题 含答案 七七文库www 77wenku Com

扇形面积计算公式怎样求扇形面积 有途教育

弧长公式 弧长公式是什么 弦长弧长计算公式 悦地带图网

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

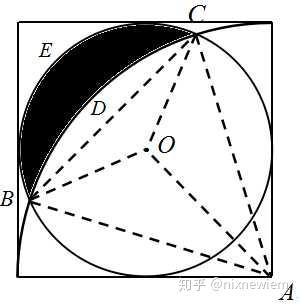
求阴影部分面积 小学题 知乎

扇形弧长公式 扇形弧长公式画法

扇形面积公式 扇形面积公式画法

扇形面积 周长 弧长公式 雨露学习互助

扇形面积公式 腾讯视频

Incoming Term: 扇形面積公式高中,